GEOMETRIA

1. El triángulo

1.1 Propiedades y tipos de triángulos

Clasificación de triángulos según sus lados

 Triángulo equilátero

Si sus tres lados tienen la misma longitud (los tres ángulos internos miden 60º grados).

Triángulo isósceles

Si tiene dos lados de la misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida.

Triángulo escaleno

Si todos sus lados tienen longitudes diferentes. En un triángulo escaleno no hay ángulos con la misma medida.

Clasificación de triángulos según sus ángulos

Triángulo Rectángulo

Si tiene un ángulo interior recto de 90º. A los dos lados que conforman el ángulo recto se les denomina catetos y al otro lado hipotenusa.

Triángulo obtusángulo

Si uno de sus ángulos es obtuso (mayor de 90º); los otros dos son agudos (menor de 90º).

Triángulo acutángulo

Cuando sus tres ángulos son menores a 90º; el triángulo equilátero es un caso particular de triángulo acutángulo.

Triángulo equiángulo

Normalmente se llama Triángulo equilátero y ya se ha comentado anteriormente.

Propiedades de los triángulos

 

Triángulos

1.2  Rectas y puntos notables en el triángulo

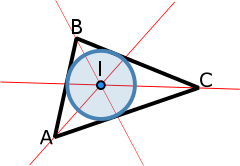
Incentro:
Es el punto central del triángulo, en el que todas las bisectrices se cortan

 

Circuncentro:
Es el centro de la circunferencia circunscrita del triángulo y es el punto de corte de las mediatrices del triángulo.

Ortocentro:
Es el punto en el que coinciden las tres alturas del triángulo.

Baricentro:
Es el punto en el que coinciden las medianas del triángulo.
Una mediana: es el segmento que une un vértice con el punto medio del lado opuesto.

1.3 El Teorema de Pitágoras

Lo que dice éste es que si queremos calcular la hipotenusa (a) de un triángulo rectángulo, lo único que tenemos que hacer es sumar  los catetos al cuadrado cada uno (b y c) y hacer la raíz cuadrada de éstos.

 

1.4 El teorema de Tales

Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado.

 2. Lugares geométricos

2.1 ¿Qué es un lugar geométrico?

Un lugar geométrico es un conjunto de puntos que cumplen determinadas condiciones o propiedades geométricas.

Algunos lugares geométricos son:

• Circunferencia.
• Elipse.
• Parábola.
• Hipérbola.

2.2 La mediatriz y la bisectriz

-La mediatriz de un segmento es una línea recta, que es perpendicular a dicho segmento, trazada por su punto medio.

-La bisectriz de un ángulo es la semirrecta, que pasa por el vértice del ángulo y lo divide en dos partes iguales.

2.3 Las cónicas

2.3.1 ¿Qué es una cónica?

Una cónica es una curva plana obtenida al cortar el cono con un plano. El ángulo que forma el plano con el eje del cono, comparado con el ángulo que forman el eje y la generatriz del cono, determina las distintas clases de cónicas.
Hay 4 tipos:

2.3.2 La circunferencia

La circunferencia es el lugar geométrico de los puntos de un plano, en la que todos los puntos que forman la circunferencia, están a la misma distancia del centro.  

2.3.3 La elipse

Es una curva plana, simple y cerrada.

• Método del jardinero

Lo que quiere decir el método del jardinero es que se atan los dos extremos de un hilo a dos chinchetas clavadas en los focos, y se mantiene el hilo tenso con un lapicero mientras vamos deslizándolo. La curva trazada corresponde con una elipse.

• Mesa de billar elíptica 

El billar elíptico se trata de una mesa de billar en la que las bandas rectas han sido sustituidas por una única banda contínua de forma elíptica, cualquier bola lanzada desde un foco, o que pase por él, acaba pasando por el otro foco después de rebotar en la banda.

2.3.4 La hipérbola

.

Es una sección cónica, una curva abierta de dos ramas obtenida cortando un cono recto por un plano oblicuo al eje de simetría, y con ángulo menor que el de la generatriz respecto del eje de revolución.

• La lámpara hiperbólica

Las figuras sobre la pared, formadas por la luz de la lámpara, se pueden reproducir experimentalmente tomando las medidas de cualquier lámpara del tipo de lámpara que tengamos en casa y de su posición relativa a la pared.

      

2.3.5 La parábola

Una parábola es la sección cónica resultante de cortar un cono recto con un plano, cuyo ángulo de inclinación respecto al eje del cono sea igual al de su generatriz.

        

•  La antena parabólica

Son las antena que se caracteriza por llevar un reflector parabólico, cuya  superficie en realidad es un paraboloide de revolución.




                                                   

• El horno solar

El horno solar es una estructura que usa energía solar concentrada para producir altas tª usualmente para usos industriales.

• El espejo parabólico

 Un espejo parabólico, es aquel que tiene una forma de antena parabólica, 

3. Movimientos en el plano

3.1 Las traslaciones y ¿qué es un vector?

La traslación son un movimiento directo de uno o varios puntos, que mantienen la forma y el tamaño de las figuras.

Un vector es un elemento que transporta uno o varios puntos, de un lugar a otro.                          

3.3 Giros

3.4 Simetría ejercicios

 

3.4.1 Dado el triángulo de vértices A (-2, 2), B (6, -1) y C (7, 5) se pide:

a. Dibujar el triángulo

b. Hallar el triángulo simétrico respecto del centro de simetría O (0, 0)

c. Hallar el triángulo simétrico del eje OX

3.4.3 Carlos y Fernando están jugando al billar. En un determinado momento las bolas se encuentran en las posiciones indicadas por el dibujo. Indica el camino que debe seguir la bola A para que rebotando en la banda MQ golpee a la bola B. 

Indica el camino que debe seguir la bola A para que rebotando en la banda NP y PQ golpee a la bola B.

3.5 Frisos, mosaicos y cenefas

-Frisos: El friso es el conjunto de molduras que coronan un edificio.

-Mosaicos: El mosaico es un conjunto de pequeñas piezas, llamadas teselas(figuras geométricas), que  forman una obra decorativa.

-Cenefas: La cenefa es un mosaico construido mediante traslaciones de distintas figuras.

4. Resumen de áreas y volúmenes de figuras conocidas

5. La esfera y el globo terráqueo

5.1 Elementos principales de la esfera

• Centro: Es el punto en el que coincide cualquier línea que dibujes desde la esfera.

• Radio: Es la distancia que hay desde el centro a cualquier punto de la esfera. Es decir, es la mitad de la distancia del diámetro.

• eje: Linea imaginaria  que pasa por el centro y sobre la que rota la esfera

• Diámetro: Es la cuerda que pasa por el centro.

• Polos: Son los puntos del eje de giro que quedan sobre la superficie esférica.

 

5.2 Elementos de la esfera terrestre

 

5.4 El método de Eratóstenes para calcular el diámetro de la circunferencia terrestre

 Un vídeo que puede ayudarte a comprender este punto es este:

Lo que hizo Erastótenes fue poner una estaca en un lugar a una hora determinada para que no se formase su propia sombra y otra , en otro lugar , sitio en el que a esa hora hacía sombra.
Y con esos datos fue capaz de calcular el diámetro de la Tierra.